جینسن نامساوات

Jensen's inequality generalizes the statement that a secant line of a convex function lies above the graph.

ریاضیات میں جینسن نامساوات نسبت کرتی ہے تکامل کی محدب دالہ کی قدر کو محدب دالہ کے تکامل سے۔

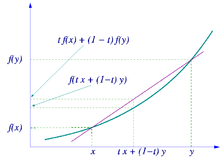
جینسن نامساوات اس بیان کو جامع بناتی ہے کہ محدب دالہ کی قاطع لکیر اُوپر پڑی ہوتی ہے دالہ کے مخطط کے۔

احتمال نظریہ کے تناظر میں یہ اس ہئیت میں پیش کی جاتی ہے: اگر X ایک تصادفی متغیر ہے اور $\varphi$ ایک محدب دالہ، تو $\varphi\left(\mathbb{E}\left[X\right]\right) \leq \mathbb{E}\left[\varphi(X)\right].$

E=mc2     اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے     ریاضی علامات