تفاعل (ریاضیات)

| اصطلاح | term |
|---|---|
|
تفاعل |
function |

ریاضیات میں تفاعل یہ تصور ہے کہ ایک قدر (تفاعل کا ادخال) سے دوسری قدر (تفاعل کا اخراج یا قدر) مکمل طور پر معلوم ہو جاتی ہے۔ تفاعل ہر ادخال کو صرف ایک اخراج قدر تفویض کرتی ہے۔ استدلال اور تفاعل کی قدر حقیقی عدد ہو سکتے ہیں یا کسی مجموعہ کے ارکان۔ حقیقی عدد کی صورت میں اکثر اوقات تفاعل کا کلیہ لکھا جا سکتا ہے اور اس کے گراف کی کارتیسی متناسق میں خاکہ کشی کی جا سکتی ہے۔ تصویر میں تفاعل f کا کلیہ

|
ہے، جہاں x افقی محور پر ہے اور y عمودی محور پر۔ اس تفاعل کے لیے استدلال x کوئی بھی حقیقی عدد ہو سکتا ہے۔ تصویر سے ظاہر ہے کہ اس تفاعل کا اخراج y غیر منفی حقیقی عدد ہوتا ہے۔
ریاضیاتی تعریف[ترمیم]
 |
|
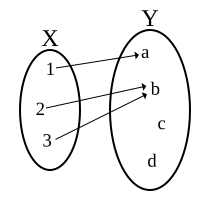
رسمی تعریف: ریاضیات میں تفاعل f ایک قاعدہ ہے جو مجموعہ X کے ہر رکن x کو مجموعہ Y کا صرف ایک رکن f(x) تفویض کرتا ہے۔
تصویر سے ظاہر ہے کہ X کے ایک سے زیادہ ارکان کو Y کا ایک ہی رکن تفویض کیا جا سکتا ہے (مگر X کے ایک رکن کو Y کے دو ارکان تفویض کرنے کی اجازت نہیں)۔
مجموعہ X کو تفاعل کا ساحہ کہا جاتا ہے۔ مجموعہ Y کے رکن f(x) کو تفاعل f کی x پر قدر بولتے ہیں۔ رکن x کو تفاعل f کا استدلال کہا جاتا ہے۔ ساحہ پر x کی تمام اقدار پر تفاعل f سے ملنے والی مجموعہ Y پر تمام اقدار f(x) کو تفاعل کا حیطہ کہتے ہیں۔ واضح رہے کہ عام طور پر تفاعل کا حیطہ، مجموعہ Y کا ذیلی مجموعہ ہو گا۔
علامتی طور پر لکھتے ہیں
یعنی f تفاعل X کو Y میں لے جاتا ہے اور
x کو f(x) نقش کرتا ہے۔
جائزہ[ترمیم]
تفاعل کا علم میں کثرت استعمال کی وجہ سے کچھ رواج راہ پا گئے ہیں۔ تفاعل کے ادخال کی علامت کو اکثر"ناتابع متغیر" یا استدلال کہتے ہیں اور حرف x کی علامت سے لکھتے ہیں یا اگر وقت کا تفاعل ہو، تو حرف t کی علامت۔ اخراج کی علامت کو "تابع متغیر" یا "تفاعل کی قدر" کہتے ہیں اور اکثر حرف y کی علامت سے لکھتے ہیں۔ تفاعل خود کو عموماً f کہتے ہیں اور اس طرح علامت y=f(x) سے مراد ہے کہ تفاعل f کی ادخال کا نام x ہے اور اخراج y نامی ہے۔

تفاعل کو آلہ کے طور پر دیکھنا مفید رہتا ہے۔ آلہ میں x داخل ہو، تو آلہ اسے بطور ادخال منظور کرے گا اور تفاعل f کے قاعدہ کے مطابق f(x) پیدا کرے گا، جو آلہ میں سے اخراج ہو گا۔ اس لیے ہم تخیل کر سکتے ہیں کہ ساحہ تمام ممکنہ ادخال ہیں اور حیطہ تمام ممکنہ اخراج۔
عام زندگی میں بیشتر اوقات تفاعل کا ساحہ اور حیطہ اعداد کا ذیلی مجموعہ ہوتے ہیں اور اکثر حقیقی اعداد۔ اس صورت میں تفاعل کا گراف بنا کر تصور کرنا آسان رہتا ہے۔
تفاعلات کی ترکیب[ترمیم]

| اصطلاح | term |
|---|---|
|
سِرک |
shift |
دو تفاعلات کی ترکیب سے نئی تفاعل وجود میں آ سکتی ہے جسے ترکیب تفاعل کہیں گے۔
دو تفاعل f اور g ہوں، ہم f کے ساحہ میں جُز x سے f کے حیطہ میں جُز y=f(x) تک پہنچتے ہیں۔ اب اگر جُز y تفاعل g کے ساحہ میں ہو تو ہم اس پر تفاعل g کے استعمال سے تفاعل g کے حیطہ میں جُز z=g(y) تک پہنچتے ہیں۔ نتیجہ نئی تفاعل h(x)=g(f(x)) ہے، جو تفاعل f کو تفاعل g میں ڈالنے سے بنی ہے۔ اسے f اور g کی ترکیب کہتے ہیں اور لکھتے ہیں۔ تفاعل f کے ساحہ کو X، تفاعل f کے حیط اور تفاعل g کے ساحہ کو Y اور تفاعل g کے حیطہ کو Z، کہتے ہوئے ہم علامتی طور پر یوں لکھ سکتے ہیں:
خیال رہے کہ ترکیبِ تفاعل میں ترتیب اہم ہے، پہلے تفاعل f استعمال ہوئی اور اس کے اخراج پر تفاعل g استعمال کی گئی۔ میکانیکی طور پر ترکیب کو تصویر میں دکھایا گیا ہے۔ تفاعل کا ساحہ وہ تمام ہیں جن کے لیے y=f(x) تفاعل g کے ساحہ میں ہیں۔ خیال رہے کہ عام طور پر
مقلوب تفاعل[ترمیم]
تعریف: کسی تفاعل کو واحد الواحد تفاعل کہا جائے گا اگر یہ کوئی قدر دو بار اختیار نہ کرے، یعنی
- جب بھی
اگر تفاعل کا ساحہ اور حیطہ حقیقی عدد ہوں، تو واحد الواحد تفاعل افقی لکیر اختبار پر پورا اترے گی۔
اگر f واحد الواحد تفاعل ہے جس کا ساحہ X اور حیطہ Y ہے، تو اس کی مقلوب تفاعل کا ساحہ Y اور حیطہ X ہو گا اور درج ذیل خاصے سے تعریف ہو گی
کسی بھی کے لیے۔ (یاد رہے کہ سے مراد ہرگز نہیں۔ کے لیے کی علامت استعمال ہوتی ہے۔)
شناخت تفاعل[ترمیم]
ایسی تفاعل جو مجموعہ X کے رکن x کو x ہی تفویض کرے کو شناخت تفاعل کہتے ہیں اور عموماً لکھتے ہیں:
واحد الواحد تفاعل f جس کا ساحہ X ہو، کے لیے
تفاعل کا استحالہ[ترمیم]
اگر تفاعل کا ساحہ اور حیطہ دونوں حقیقی اعداد ہوں، یعنی ، تو پھر تفاعل کا گراف بنایا جا سکتا ہے اور اس کی استحالہ خصوصیت پڑھی جا سکتی ہیں۔ ذیل میں c حقیقی عدد ہے:


افقی سرکنا[ترمیم]
- اگر
c>0ہو، تو تفاعلf(x-c)، تفاعلf(x)کی دائیں سرکی صورت ہے۔ - اگر
c>0ہو، تو تفاعلf(x+c)، تفاعلf(x)کی بائیں سرکی صورت ہے۔
منعکس[ترمیم]
- تفاعل
f(x)کو عمودی دھرا کے حوالہ سے منعکس کرنے سے تفاعلf(-x)بنتا ہے۔
کھینچنا اور دابنا[ترمیم]
- اگر
c>1ہو، تو تفاعلf(cx)، تفاعلf(x)کی اُفقی دابی صورت ہے۔ - اگر
c>1ہو، تو تفاعل ، تفاعلf(x)کی اُفقی کھینچی صورت ہے۔[1]
E=mc2 اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے ریاضی علامات
| ویکی ذخائر پر تفاعل (ریاضیات) سے متعلق سمعی و بصری مواد ملاحظہ کریں۔ |
- ↑ A. D. Aleksandrov، A. N. Kolmogorov، مدیران (1999)۔ Mathematics: Its Content, Methods and Meaning۔ Courier Dover

![{\displaystyle {\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367545798d4c1d7748410deb9d03ea9faf400d6d)














![{\displaystyle \ [f(x)]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a92a7b03073d1b7f76f54a4d5e40e4755d0519d)





