گراف (ریاضی)

ریاضی میں گراف نقاط اور لکیروں پر مشتمل ہوتا ہے، ایسا کہ ہر لکیر صرف دو نقاط کو جوڑتی ہے۔ کوئی بھی نقاط کا جوڑا لکیر کے ذریعہ جوڑا جا سکتا ہے۔ ایک نقطہ اپنے آپ سے بھی لکیر کے ذریعہ جوڑا جا سکتا ہے (اسے مدور کہتے ہیں)۔ نقاط کو راس کہتے ہیں اور جوڑنے والی لکیر کو کنارہ۔ ایک کنارہ صرف دو راس کو آپس میں جوڑتا ہے۔
مثال کے طور پر تصویر 2 میں گھر کا نقشہ دیا ہے۔ اس نقشہ کا گراف بنانے کے لیے ہر کمرے کو راس (دائرہ) سے دکھایا گیا ہے۔ جن دو کمروں کے درمیان دروازہ ہے، گراف میں وہ کنارہ سے جڑے دکھائے گئے ہیں۔ راس پر کمرے کا عدد لکھا گیا ہے۔ اس طرح یہ کمروں کے اتصال کا گراف ہے۔



| اصطلاح | term |
|---|---|
|
گراف |
graph |
گراف اور اس کی اقسام[ترمیم]
تعریف: گراف G مشتمل ہوتا ہے غیر خالی مجموعہ پر جس کے ارکان راس ہوتے ہیں اور ان ارکان کے جوڑوں کی نامرتب فہرست پر، جنہیں کنارے کہا جاتا ہے۔ راس کے مجموعہ کو گراف کا "راس مجموعہ" کہتے ہیں اور V(G) لکھتے ہیں۔ کناروں کی فہرست کو "کنارہ فہرست" کہتے ہیں اور E(G) لکھتے ہیں۔ اگر u اور v راس ہوں، تو کنارہ uv یا vw، راس u اور v کو آپس میں "مِلاتا" ہے۔
تصویر 1 میں
تعریف: اگر دو راس کو ایک سے زیادہ کنارے جوڑتے ہوں، تو انھیں متعدد کنارے کہا جاتا ہے۔ اگر کنارہ راس کو اپنے آپ سے جوڑے تو اسے مدور کہا جاتا ہے۔ تصویر 3 میں سرخ رنگ میں تین "متعددکنارے" دکھائے گئے ہیں۔ نیلے رنگ میں "مدور" ہے۔

سادہ گراف[ترمیم]
ایک گراف جس میں متعددکنارے اور مدور نہ ہوں کو سادہ گراف کہا جائے گا۔
متصل گراف[ترمیم]
گراف جو صرف ایک ٹکرے میں ہو کو متصل گراف کہتے ہیں ورنہ نامتصل گراف۔
 |  |
ذیلی گراف[ترمیم]
تعریف: گراف G کا راس مجموعہ V(G) اور کنارہفہرست E(G)ہو۔ گراف کا ذیلیگراف ایسا گراف ہے جس کی تمام راس V(G) میں ہوں اور تمام کنارے E(G) میں ہوں۔
تعریف: اگر G گراف ہے بغیر مدور کے اور v اس کا ایک قمہ ہے۔ قمہ v کا درجہ اس میں ملنے والے کناروں کی تعداد ہے اور اسے deg(v) لکھتے ہیں۔ تصویر 1 میں قمہ 5 کا درجہ 3 ہے۔
باقاعدہ گراف[ترمیم]
اگر گراف کی تمام راس کے درجات برابر ہوں، تو گراف کو باقاعدہ گراف کہیں گے۔ اگر درجہ r ہو تو گراف کو باقاعدہگراف درجہ r کے ساتھ کہیں گے۔
مصافحہ مبعث[ترمیم]
گراف مٰیں تمام راس کے درجات کی حاصل جمع دوگنی ہوتی ہے کناروں کی تعداد کے ۔
- راس کے درجات کا حاصلجمع جفت عدد ہوتا ہے۔
- ایسی راس جن کا درجہ طاق عدد ہو، کی تعداد جفت عدد ہوتی ہے۔
- باقاعدہگراف درجہ r کے ساتھ، کی راس کی تعداد n ہو، تو کناروں کی تعداد ہو گی۔
| اصطلاح | term |
|---|---|
|
مکمل |
complete |
مکمل گراف[ترمیم]
- تفصیلی مضمون مکمل گراف
ایسا گراف جس کے کوئی بھی دو واضح راس صرف اور صرف ایک کنارے سے جڑی ہوں، کو مکمل گراف کہا جاتا ہے۔ مکملگراف جس کی راس کی تعداد n ہو کو لکھتے ہیں۔
عدیمہ گراف[ترمیم]
جس گراف میں کوئی کنارے نہ ہوں کو عدیمہ گراف کہتے ہیں۔ عدیمہگراف جس کی راس کی تعداد n ہو کو لکھتے ہیں۔ یہ گراف باقاعدہ ہو گا درجہ 0 کے ساتھ۔
 |  |
دورہ گراف[ترمیم]
گراف جس میں صرف ایک دورہ ہو کو دورہ گراف کہتے ہیں۔ دورہگراف جس کی راس کی تعداد n ہو کو لکھتے ہیں۔

راستہ گراف[ترمیم]
گراف جس میں صرف ایک رستہ ہو کو راستہگراف کہتے ہیں۔ رستہ گراف جس کی راس کی تعداد n ہو کو لکھتے ہیں۔

دوحصائی گراف[ترمیم]
ایسا گراف جس کے راس مجموعہ کو دو ذیلی مجموعات A اور B میں بانٹا جا سکے اس طرح کہ ہر کنارہ مجموعہ A کے کسی قمہ کو مجموعہ B کے کسی قمہ سے جوڑتا ہو۔ تصویر میں راس کے ذیلی مجموعات کو "نیلے" اور "سرخ" رنگ میں دکھایا گیا ہے۔
| اصطلاح | term |
|---|---|
|
سمتی گراف |
directed graph (digraph) |
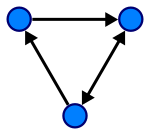
سمتی گراف[ترمیم]
- تفصیلی مضمون سمتی گراف
ایسا گراف جس میں کناروں کی سمت مقرر ہو جو تیر کے نشان سے دکھائی جاتی ہے۔ اسے یوں سمجھا جا سکتا ہے جیسے مقام ا اور ب کے درمیان ریلگاڑی مقام ا سے ب کی طرف چلتی ہو مگر دوسری جانب نہیں۔
- تعریف: سمتی گراف D مشتمل ہوتا ہے ایک مجموعہ جسے راس کہتے ہیں اور راس کے جوڑوں کی مرتب فہرست جنہیں تیر کہتے ہیں۔ راس کو "راس مجموعہ"
V(D)لکھتے ہیں اور تیروں کو "تیر فہرست"A(D)لکھتے ہیں۔ اگر a اور b راس ہیں تو تیر ab کی سمت a سے b ہوتی ہے یا a کو b سے جوڑتا ہے (مگر b کو a سے نہیں جوڑتا)۔

موزون گراف[ترمیم]
موزون گراف، ایسا گراف جس میں ہر کنارے کے ساتھ ایک مثبت عدد نتھی کر دیا جائے جو اس کا وزن کہلائے۔ مثلاً اگر راس شہر ہوں تو وزن دو شہروں کے درمیان فاصلہ۔
| اصطلاح | term |
|---|---|
|
متشاکل |
isomorphic |


متشاکل گراف[ترمیم]
دو گراف G اور F کو متشاکل کہا جائے گا اگر G کو F میں تبدیل کیا جا سکے اس کے ملصق کی جگہ تبدیل کر کے۔ دوسرے الفاظ میں اگر G اور F کی راس میں ایسا ارتباط واحد الواحد ہو کہ G میں کسی بھی "راس جوڑے" کو جوڑنے والے کنارے کی تعداد برابر ہو F میں ارتباطی "راس جوڑے" کو جوڑنے والے کناروں کی تعداد کے ۔
مزید دیکھیے[ترمیم]
بیرونی روابط[ترمیم]
E=mc2 اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے ریاضی علامات










