مشتق شکن
| اصطلاح | term |
|---|---|
|
مشتق شکن |
antiderivative |
احصا میں دالہ f کا مشتق شکن یا غیرواضح تکامل[2]
ایسی فنکشن F ہے جس کا مشتق f کے برابر ہو، یعنی F ′ = f ۔
مشتقشکن کی تقویم کے عمل کو مشتقشکنی (یا غیرواضح تکامل) کہتے ہیں۔ مشتق شکن کا رشتہ واضح تکامل سے حسابان کے بنیادی قضیہ کے ذریعہ بنتا ہے: فنکشن کا وقفہ پر واضح تکامل برابر ہے اس فنکشن کے مشتقشکن کی وقفہ کے کناروں پر اقدار کے فرق کے ۔
قواعد اور کلیہ[ترمیم]
تفریقی شکن عملیت ہے فنکشن کے تمام مشتق شکن ڈھونڈنے کا۔ علامت تعبیر کرتا ہے مشتق شکن عالج کو۔
-
- جہاں
فنکشن ƒ کا جامع مشتق شکن F(x) + C ہے۔ دائم C استعمال ہوتا ہے کیونکہ دائم کامشتق ہمیشہ 0 ہوتا ہے۔
چونکہ تفریقیشکن مقلوب عالج ہے تفریقی کا، تفریقی شکن کے قضیہ اور قواعد تفریقی کے قواعد و قضیہ سے اخذ کیے جاتے ہیں۔ چنانچہ، ذیل کے قضیہ تفریقی کے ارتباطی قضیہ سے اخذ کیے جا سکتے ہیں:
- جامع تفریقی شکن قاعدہ:
دائم بضرب فنکشن کا جامع مشتق شکن ہوتا ہے دائم بضرب * فنکشن کا جامع مشتق شکن:
- اگر ƒ اور g اُسی وقفہ پر متعرف ہوں، تو ƒ اور g کے حاصل جمع کا مشتق شکن برابر ہو گا ƒ اور g کے مشتق شکنوں کے حاصل جمع کا:
- اگر n حقیقی عدد ہو، تو
E=mc2 اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے ریاضی علامات
- ↑
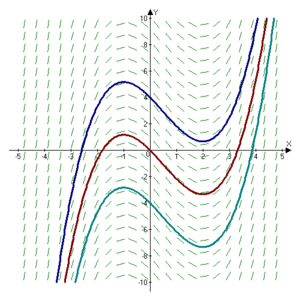
اس طرح کی تصویر بنانے کے لیے مکسما کا استعمال کیا جا سکتا ہے:
/* Maxima -- http://maxima.sourceforge.net */
- load("plotdf");
- plotdf((x^3)/3-(x^2/2)-x,[x,-5,5]);
- ↑ Antiderivatives are also called general integrals, and sometimes integrals. The latter term is generic, and refers not only to indefinite integrals (antiderivatives), but also to definite integrals. When the word integral is used without additional specification, the reader is supposed to deduce from the context whether it is referred to a definite or indefinite integral. Some authors define the indefinite integral of a function as the set of its infinitely many possible antiderivatives. Others define it as an arbitrarily selected element of that set. Wikipedia adopts the latter approach.






![{\displaystyle \int [f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dc2c6e2acadf432d22ca42bc6a21af25e48e64d)
