تکامل

تکامل ریاضیات میں ایک اہم تصور ہے جو تفرقی کے ہمراہ احصا میں ایک اکبر عالج ہے۔ حقیقی متغیر کی فنکشن f اور حقیقی لکیر پر وقفہ دیا ہو، تو واضح تکامل
غیر رسمی طور پر xy-مسطح میں وہ مثبت/منفی نشانذدہ باقیماندہ علاقے کا رقبہ ہے جو دالہ f کے گراف اور عمودی لکایر x = a اور x = b کے درمیان ہے۔
| اصطلاح | term |
|---|---|
|
واضح |
definite |
تکامل کی اصطلاح سے مراد مشتق شکن F بھی ہو سکتا ہے جس کا مشتق دی گئی فنکشن f ہے۔ اس صورت میں اسے غیرواضح تکامل کہتے ہیں، جبکہ یہاں ہم واضح تکامل پر بحث کریں گے۔ کچھ لکھاری غیرواضح تکامل اور مشتقشکن میں تمیز کرتے ہیں۔
تکامل کے اصول 17ویں صدی کے آخر میں لائبنز اور نیوٹن نے علاحدہ اپنے طور پر کلیات کیے تھے۔ قضیہ بنیادی حسابان کے ذریعہ تکامل کا جوڑ تفرقی سے بنتا ہے: اگر f ایک استمری حقیقی-قدری فنکشن ہو جو بند وقفہ [a, b] پر تعریف شدہ ہو، تو جیسے ہی f کا مشتقشکن F معلوم ہو گا، فنکشن f کا اس وقفہ پر تکامل یوں دیا جائے گا:
تکامل اور مشتق آساسی اوزار بن گئے ہیں حسابان کے اور ان کی سائنس اور ہندسہ میں لاتعداد اطلاقیات ہیں۔ تکامل کی بامشقت ریاضیاتی تعریف ریمان نے دی۔ یہ ایک حدی طریقہ ہے جس میں منحنی لکیری علاقہ کا رقبہ تقرب کیا جاتا ہے، علاقے کو پتلی عمودی سِلوں میں توڑ کر۔ انیسویں صدی میں تکامل کے زیادہ ثقیف تصورات ظاہر ہونا شروع ہوئے، جہاں فنکشن کی قسم اور جس ساحہ پر تکامل انجام دیا جائے کو جامع بنایا گیا۔ ایک لکیری تکامل دو یا تین متغیروں کی فنکشن کے لیے تعریف کیا جاتا ہے اور تکامل کے وقفہ [a, b] کو مسطح یا فضاء میں دو نقطوں کو جوڑنے والی کسی خاص منحنی سے بدل دیا جاتا یے۔ سطح تکامل میں منحنی کی جگہ سہ العباد فضاء میں سطح کا ٹکرا بدیل کر دیا جاتا ہے۔ تفرقی ہئیتوں کے تکامل تفرقی ہندسیہ میں بنیادی کردار کھیلتے ہیں۔ یہ جامع شکلیں پہلے طبیعیات کی ضرورتیں پوری کرنے کے لیے اُبھریں اور یہ کئی طبیعیاتی قوانین کی کلیات میں اہم کردار ادا کرتے ہیں، نمایاں ً برقی حرکیات میں۔ تکامل کے کئی جدید تصورات ہیں۔ ان میں سب سے عام تکامل کا تصور تجریدی ریاضیاتی نظریہ پر اساس ہے جسے لابیگ تکامل کہتے ہیں اور جسے ہنری لابیگ نے ترقیآیا۔
تاریخ[ترمیم]
پیش حسابان تکامل[ترمیم]
تکامل کو قدیم مصر تک (قریبا 1800 قبل مسیح) تلاش کیا جا سکتا ہے۔ ماسکو ریاضی البَردی سے معلوم ہوتا ہے کہ ان کو اہرام کے حجم کا کلیہ کا علم تھا۔ سب سے پہلا نظامیاتی طریقہ رقبہ اور حجم نکالنے کے لیے شکلوں کو لامتناہی تعداد میں ایسے ٹکروں میں توڑنا تھا جن کا رقبہ یا حجم معلوم ہوتا۔ اس طرح کے طریقے یونانیوں اور چینیوں کو معلوم تھے۔[1]
اس کے بعد اکبر قدم عراق میں 11 ویں صدی کےاسلامی ریاضیدان ابن الحیثم نے اپنی کتاب کتابِ بصریات میں اٹھایا، جو اب الحیثم مسئلہ کہلاتا ہے، جس میں درجہ چار کی مساوات بنتی ہے۔ اس مسئلہ کے حل کے دوران، اس نے تکامل انجام دیا تاکہ مکافی مجسم کا حجم نکال سکے۔ ریاضیاتی تحریض کے استعمال سے اس نے چوتھے درجہ تک کے کثیر رقمی کے تکامل کا کلیہ اخذ کیا۔[2] چونکہ وہ بصریات کی کتاب لکھ رہا تھا، نہ کہ ریاضی کی، اس لیے اس نے 4 سے زیادہ درجہ کے کثیر رقمی کا جامع نتیجہ تحریر نہیں کیا، جس سے بعض مورخین کو غلط فہمی ہوئی کہ الحیثم کو یہ نتیجہ معلوم نہ تھا۔
اگلی اہم پیش رفت 16ویں صدی میں ہوئی۔ کیوالیری نے method of indivisibles|لاتقیسمً کے طریقہ سے اور فرمے نے جدید حسابان کی بنیاد رکھنا شروع کی۔ 17ویں صدی میں بیرو اور تورسلی نے تکامل اور تفرق کے درمیان اتصال کی طرف اشارے کیے۔
لائبنز اور نیوٹن[ترمیم]
اگلی اہم پیش رفت 17ویں صدی میں لائبنز اور نیوٹن نے حسابان کا بنیادی قضیہ دریافت کر کے کی۔ یہ قضیہ تکامل اور تفرق کے درمیان اتصال بیان کرتا ہے۔ یہ اتصال اور نسبتاً آسان تفرق کے طرائق، کا استحصال کر کے تکامل کی حسابگری کی جا سکتی ہے۔ خاصاً یہ قضیہ ہمیں مسائل کی بہت وسیع جماعت کو حل کرنے کی اجازت دیتا ہے۔ اس کے علاوہ ان اصحاب نے جامع ڈھانچہ ترقیایا۔ اس کو صغاریہ حسابان کا نام دیا گیا، جس سے فنکشن اور استمری ساحہ کا قطعی تحلیل ممکن ہوا۔ یہ ڈھانچہ آخرکار جدید احصا بن گیا اور تکامل کی علامت لائبنز کے کام سے لی گئی ہے۔
اصطلاحیات اور علامات[ترمیم]
اگر کسی فنکشن کا تکامل ہو، تو فنکشن کو قابلِ تکامل ہے۔ جس فنکشن کے لیے تکامل کمپیوٹر کیا جائے اس فنکشن کو متکامل کہتے ہیں۔ جس علاقہ پر فنکشن کا تکامل کیا جائے اس علاقہ کو تکامل کا ساحہ کہتے ہیں۔ اگر تکامل کا ساحہ نہ دیا گیا ہو، تو اسے غیرواضح تکامل کہتے ہیں (جس کا ساحہ ہو اسے واضح تکامل سمجھو)۔ جامع طور پر متکامل ایک سے زیادہ متغیروں کا فنکشن ہو سکتا ہے اور تکامل کا ساحہ رقبہ، حجم یا بالا بُعد علاقہ بھی ہو سکتا ہے اور کو تجریدی فضاء بھی جس کی عام معنوں میں کوئی ہندسیاتی ساخت نہ ہو۔
سادہ ترین صورت، ایک حقیقی متغیر x کی حقیقی-قدر فنکشن f، وقفہ [a, b] پر، یوں تعبیر کی جاتی ہے
نشان ∫ نمائندگی کرتا ہے تکامل کی؛ a زیریں حد ہے اور b بالائی حد تکامل کی؛ فنکشن f متکامل ہے، جس کی تقویم کرنا ہے جب x وقفہ [a, b] پر تبدیل ہوتا ہے؛ اور dx تکامل کا متغیر ہے۔ صحیح ریاضیاتی علامت میں متکامل اور dx کے درمیان وقفہ ڈالا جاتا ہے (جیسا کہ دکھایا گیا ہے)۔
نظریہ کے مطابق تکامل کے متغیر dx کی تفسیر مختلف ہوتی ہے۔ مثلاً، اس کو سمجھا جا سکتا ہے محض علامت جس سے مراد ہےx تکامل کا اخرس متغیر ہے، ریمان حاصل جمع میں وزون کا عکس، ناپ (لابیگ تکامل میں)، صغاریہ (غیر -معیاری تحلیل میں) یا آزاد ریاضیاتی مقدار: تفرقی ہئیت۔
تعارف[ترمیم]
تکامل کئی ممارسی صورت حالوں میں ظاہر ہوتا ہے۔ ایک تالاب کو دیکھو۔ اگر یہ مستطیل ہے، تو اس کی لمبائی، چوڑائی اور گہرائی سے اس کو پوار بھرنے کے لیے درکار پانی کا حجم جبر کیا جا سکتا ہے، اس کی سطح کا رقبہ نکالا جا سکتا ہے (اس کو ڈھانپنے کے لیے) اور اس کے کناروں کی لمبائی (اس کے گرد رسی لگانے کے لیے)۔ مگر اگر یہ بیضوی ہو گولی پیندے کے ساتھ، تو ان تمام مقداروں کے لیے تکامل کو پکارنا پڑے گا۔ ہو سکتا ہے کہ ممارسی تقرب کافی ہو، مگر قطعی ہندسیہ کے لیے ان عناصر کی صحیح اور بامشقت اقدار چاہیے ہوتی ہیں۔
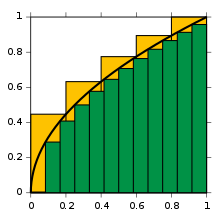
شروع کرنے کے لیے، اس منحنی y = f(x) کو دیکھو جو x = 0 اور x = 1 کے درمیان ہے اور فرض کرو کہ f(x) = √x ہے۔
- تفاعل f کے نیچے کتنا رقبہ ہے، 0 سے 1 تک وقفہ میں؟
اور اس (ابھی نامعلوم) رقبہ کو f کا تکامل کہو۔ اس تکامل کی علامت یہ ہو گی
پہلے تقرب کے طور پر اکائی مربع پر نظر ڈالو جس کی اطراف x = 0 سے x = 1 تک اور y = f(0) = 0 سے y = f(1) = 1 تک ہیں۔ اس کا مربع قطعی 1 ہے۔ تکامل کی سچی قدر اس سے کچھ کم ہوگی۔ تقربی مستطیلوں کی چوڑائی کم کر کے بہتر نتیجہ دے گا؛ تو وقفہ کو پانچ قدموں میں طے کرو، تقربی نقطے 0، 1⁄5، 2⁄5 اور اس طرح 1 تک۔ ہر قدم پر ایک ڈبہ بٹھاؤ جس کی اونچائی منحنی کا دائیں والا کونا ہو، چنانچہ
√2⁄5، √1⁄5 اور اس طرح √1 = 1 تک۔ ان مستطیلوں کے رقبہ کو جمع کر کے، ہمیں تکامل کا بہتر تقرب ملتا ہے، ناماً
غور کرو کہ ہم متناہی تعداد میں f کی اقدار بہ ضرب "اگلے دو تقربی نقطوں کا فرق" کا حاصل جمع لے رہے ہیں۔ ہم دیکھ سکتے ہیں کہ تقرب اب بھی کافی زیادہ ہے۔ زیادہ قدم استعمال کر کے تقرب بہتر ہو گی مگر قطعی نہیں ہو گی: پانچ قدموں کو بارہ سے بدل کر ہمیں رقبہ تقرب 0.6203 ملتا ہے جو بہت کم ہے۔ کلیدی خیال یہ ہے کہ تقرب کے متناہی فرق ضرب متعلقہ فنکشن اقدار سے لامتناہی باریک کی طرف جایا جائے یا صغاریہ قدم۔
تکامل کی حقیقی حسابگری کے لیے حسابان کا بنیادی قضیہ استعمال ہوتا ہے، جو تفرقی اور تکامل کے درمیان بنیادی ربط ہے۔ مربع جذر فنکشن f(x) = x1/2 پر اطلاق کے لیے یہ کہتا ہے کہ اس کا مشتق شکن F(x) = 2⁄3x3/2 لو اور سادہ F(1) − F(0)=2/3 تکامل کے جواب کے طور پر لے لو، جہاں 0 اور 1 تکامل کے وقفہ [0,1] کی سرحدیں ہیں۔ منحنی کے نیچے قطعی رقبہ یوں رسمی طور پر کمپیوٹر کیا جاتا ہے:
علامت (لمبا s جس سے مراد انگریزی 'sum' لفظ ہے)
تکامل کو بطور وزونی حاصل جمع بھانپتی ہے، فنکشن f(x) کی اقدار، بضرب صغاریہ قدم چوڑائی جسے تفریقیے کہتے ہیں اور dx کی علامت سے لکھتے ہیں۔ ضرب کی علامت نہیں لکھی جاتی۔
تکامل کی تعریف کو بامشقت بنانے کے لیے ریمان نے اسے بطور وزونی حاصل جمع کی حد تعریف کیا، اس طرح dx سے مراد فرق (قدم کی چوڑائی) کی حد ہے۔
| اصطلاح | term |
|---|---|
|
تتمہ |
tag |
رسمی تعاریف[ترمیم]
تکامل کی رسمی تعریف کے کئی طرائق ہیں، جو سب مطابقت نہیں۔ کچھ خاص صورتیں ایک تعریف کے تحت قابل تکامل ہوں مگر دوسری کے نہیں۔ عام استعمال کی تعاریف ریمان تکامل اور لابیگ تکامل ہیں۔
ریمان تکامل[ترمیم]
ریمان تکامل کو فنکشن کے رحمان حاصل جمع بلحاظ وقفہ کے تتمہ-ائی بٹوارہ کے معنوں میں تعریف کیا حاتا ہے۔ چلو [a,b] حقیقی لکیر کا بند وقفہ ہو؛ پھر اس وقفہ [a,b] کا تتمہ-ائی بٹوارہ ایک متناہی متوالیہ ہے

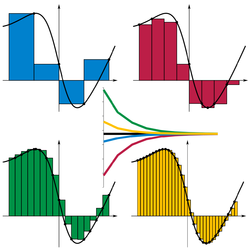
اس وقفہ [a,b] کو n ذیلی-وقفوں [xi−1, xi] میں تقسیم کرتا ہے جن کی فہرست i سے ظاہر کی گئی ہے اور ان میں سے ہر کو ایک ممتاز نقطہ ti ∈ [xi−1, xi] سے 'تتمہ' کیا گیا ہے۔ فنکشن f کا ریمان حاصلجمع بلحاظ تمتہ بٹوارہ یوں تعریف ہوتا ہے:
چنانچہ حاصل جمع کی ہر اصطلاح رقبہ ہے مستطیل کا جس کی اُونچائی فنکشن کی ممتاز نقطہ پر قدر کے برابر ہے اور چوڑائی اس ذیلی-وقفہ کی چوڑائی ہے۔ چلو Δi = xi−xi−1 ذیلی-وقفہ i کی چوڑائی ہو؛ اس تتمہ بٹوارہ کا شیکہ ان میں سے سب سے چوڑے ذیلی-وقفہ کی چوڑائی ہے، maxi=1…n Δi۔ فنکشن f کا وقفہ [a,b] پر ریمان تکامل برابر ہے S کے اگر
- تمام ε > 0 کے لیے ایسا δ > 0 وجود رکھتا ہو کہ، وقفہ
[a,b]کے کسی بھی تتمہ بٹوارہ جس کا شیکہ δ سے کم ہو، ہمارے پاس ہو
خواص[ترمیم]
لکیری[ترمیم]
- بند وقفہ
[a, b]پر قابلِ ریمان تکامل فنکشنات کا مجموعہ سمتیہ مکاں بناتا ہے، عالجہات نقطہ وار جمع اور عددیہ سے ضرب کے تحت۔ تکامل کے عالجہ کے تحت
لکیری دالہرا ہے اس سمتیہ فضاء پر۔ چنانچہ، اول، قابلِ تکامل فنکشنات کا مجموعہ بند ہے خطی اجتماع کے تحت؛ اور، دوم، لکیری تولیف کا تکامل لکیری تولیف ہے تکاملات کا،
تکامل کے لیے نامساوات[ترمیم]
بند اور محیط وقفہ [a, b] پر قابلِ ریمان تکامل دالہات کے لیے متعدد نامساوات تھامتی ہیں۔
- بالا اور زیریں حدود۔ وقفہ
[a, b]پر قابلِ تکامل فنکشن لازماً اس وقفہ پر محدود ہو گی۔ چنانچہ حقیقی اعداد m اور M ہوں گے تانکہm ≤ f (x) ≤ Mتمام کے لیے۔ چونکہ وقفہ[a, b]پر f کے نچلے اور اوپرلے حاصل جمع بالترتیبm(b − a)اورM(b − a)سے محدود ہوں گے، اس سے یہ معلوم ہوتا ہے کہ
- تفاعلات کے درمیان نامساوات۔ اگر وقفہ
[a, b]میں تمام x کے لیےf(x) ≤ g(x)ہو، تو فنکشن f کا اوپرلا اور نچلا حاصل جمع کم ہو گا بالترتیب g کے اوپرلے اور نچلے حاصل جمع سے، چنانچہ
- ذیلی وقفے۔ اگر
[c, d]ذیلی وقفہ ہو وقفہ[a, b]کا اورf(x)غیر -منفی ہو تمام x کے لیے، تو
- حاصل ضرب اور تفاعلات کی مطلق قدریں۔ اگر f اور g دو فنکشنات ہیں، تو ہم ان کے نقطہ وار حاصل ضرب، طاقتیں اور مطلق قدروں کو ملاحظہ کر سکتے ہیں:
اگر f وقفہ [a, b] پر قابلِ ریمان تکامل ہو تو یہ |f| کے لیے بھی سچ ہو گا اور:
علاوہ ازیں، اگر f اور g دونوں قابلِ ریمان تکامل ہوں تو g 2، f 2 اور fg بھی قابلِ ریمان تکامل ہوں گے اور
- یہ نامساوات، جسے کاشی شوارز نامساوات کہے ہیں، نظریہ ہلبرٹ فضاء میں اہم کردار ادا کرتی ہے، چہاں بائیں ہاتھ طرف کی وقفہ
[a, b]پر دو مربع-قابلِ تکامل تفاعلات f اور g کے اندرونی حاصل ضرب کے طور پر تشریح کی جاتی ہے۔
- منکاؤسکی نامساوات۔ فرض کرو کہ
p ≥ 1حقیقی عدد ہے اور f اور g قابلِ ریمان تکامل فنکشن ہیں۔ تو پھر|g|p،|f|pاور|f + g|pبھی قابلِ ریمان تکامل ہوں گے اور درجِ ذیل منکاوسکی نامساوات ٹھیرے گی:
رواج[ترمیم]
اس قطعہ میں f حقیقی عدد-قدر قابلِ ریمان تکامل دالہ ہے۔
وقفہ [a, b] پر تکامل
متعرف ہے اگر a < b ہو۔ اس کا مطلب ہے کہ f کے اوپرلے اور نچلے حاصل جمع بٹوارہ a = x0 ≤ x1 ≤ . . . ≤ xn = b جس کی اقدار xi بڑھ رہی ہیں، پر تقویم کیے جاتے ہیں۔ ہندساتی معنی یہ کہ تکامل "بائیں سے دائیں" چلتا ہے، وقفات [x i , x i +1] پر f کی تقویم کی جاتی ہے جہاں فہرست میں بڑا وقفہ فہرست میں چھوٹے وقفہ کے دائیں طرف پڑا ہوتا ہے۔ وقفہ کے کنارے a اور b کو f کی تکامل کی حدیں کہا جاتا ہے۔
اگر a > b ہو پھر بھی تکامل تعریف کیا جا سکتا ہے:
- تکامل کی حدوں کو پلٹنا۔ اگر
a > bہو تو تعریف کرو
اگر a=b ہو تو یہ متقاضی کرتا ہے
- صفر لمبائی کے وقفہ پر تکامل۔ اگر a حقیقی عدد ہو تو
- تکامل کے وقفات کی جمعائی۔ اگر وقفہ
[a, b]کا عُنصر c ہو، تو
- ↑ Marilyn Shea (May 2007)، Biography of Zu Chongzhi، University of Maine، 14 جون 2010 میں اصل سے آرکائیو شدہ، اخذ شدہ بتاریخ 09 جنوری 2009
Victor J. Katz (2004)، A History of Mathematics, Brief Version، Addison-Wesley، صفحہ: 125–126، ISBN 978-0-321-16193-2 - ↑ Victor J. Katz (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163–174 [165–9 & 173–4]
E=mc2 اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے ریاضی علامات
| ویکی ذخائر پر تکامل سے متعلق سمعی و بصری مواد ملاحظہ کریں۔ |

![{\displaystyle \ [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4c40bbeaa2f59e60b6259cebe2479bc24396f0)












![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)









