| اصطلاح
|
term
|
اندرونی حاصل ضرب
اندرونی حاصل ضرب فضاء
|
Inner product
Inner product space
|
ایسی لکیری فضا جس میں "اندرونی حاصل ضرب" تعریف کیا ہوا ہو، کو اندرونی حاصل ضرب فضا کہتے ہیں۔
تعریف: اندرونی حاصل ضرب
"اندرونی حاصل ضرب" ایک فنکشن ہے، جو سمتیہ مکاں V کے سمتیہ u اور v کے جوڑے کے ساتھ ایک اصلی عدد  کی نسبت اس طرح جوڑتی ہے کہ نیچے دیے قواعد پورے ہوں۔ یہاں u, v, w سمتیہ ہیں اور
کی نسبت اس طرح جوڑتی ہے کہ نیچے دیے قواعد پورے ہوں۔ یہاں u, v, w سمتیہ ہیں اور  ایک سکیلر (تمام اعداد میدان
ایک سکیلر (تمام اعداد میدان  پر ہیں)
پر ہیں)
 متناظر
متناظر جمع
جمع ہم جنسیت
ہم جنسیت مثبت ہونا
مثبت ہونا "اندرونی حاصل ضرب" صفر ہو گی، اگر بشرطِ اگر، جب سمتیہ خود صفر ہو۔
"اندرونی حاصل ضرب" صفر ہو گی، اگر بشرطِ اگر، جب سمتیہ خود صفر ہو۔
اقلیدیسی فضا پر "اندرونی حاصل ضرب[ترمیم]
| اصطلاح
|
term
|
| اقلیدسی فضاء
|
Euclidean space
|
اقلیدس سمتیہ مکاں  پر سمتیہ
پر سمتیہ
![{\displaystyle \mathbf {u} =\left[{\begin{matrix}u_{0}\\u_{1}\\\vdots \\u_{n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7979838a30debfcc4f08509bc160e07af4b422) اور سمتیہ
اور سمتیہ
![{\displaystyle \mathbf {v} =\left[{\begin{matrix}v_{0}\\v_{1}\\\vdots \\v_{n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44ec0b66ead11ed07c9a79ed69e71ff2067d349d) کے درمیان ایک
کے درمیان ایک
- "اندرونی حاصل ضرب" یوں تعریف کیا جا سکتا ہے :

اب یہ آسانی سے تسلی کی جا سکتی ہے کہ یہ تعریف قواعد 1 تا 5 پر پورا اترتی ہے۔ (یہاں t پلٹ (میٹرکس) کو ظاہر کرتا ہے۔ )
- اس اندرونی ضرب کی زیادہ عام صورت اس طرح تعریف کی جاتی ہے۔ اگر A ایک مقلوب میٹرکس ہو، تو "اندرونی حاصل ضرب" یوں تعریف کرتے ہیں :

اب یہ آسانی سے تسلی کی جا سکتی ہے کہ یہ تعریف قواعد 1 تا 5 پر پورا اترتی ہے۔ (یہاں t پلٹ (میٹرکس) کو ظاہر کرتا ہے۔ ) یاد رہے کہ میٹرکس ضرب لکیری استحالہ بناتی ہے۔ اس مساوات کو ہم یوں لکھتے ہیں

یہ زور دینے کے لیے کہ R ایک متناظر میٹرکس ہے۔
فضا میں سمتیہ کی لمبائی[ترمیم]
تفصیلی مضمون : امثولہ (ریاضی)
لکیری فضا  میں ایک سمتیہ
میں ایک سمتیہ  کی لمبائی کو
کی لمبائی کو  لکھتے ہیں اور یہ سمتیہ کا اپنے ساتھ "اندرونی حاصل ضرب" کے جزر سے یوں تعریف کی جاتی ہے :
لکھتے ہیں اور یہ سمتیہ کا اپنے ساتھ "اندرونی حاصل ضرب" کے جزر سے یوں تعریف کی جاتی ہے :

سمتیہ کی لمبائی کو سمتیہ کا اُمثولہ بھی کہتے ہیں۔ انگریزی میں اسے سمتیہ کی norm کہتے ہیں۔
اقلیدسی فضا میں سمتیہ کی لمبائی[ترمیم]
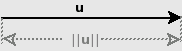
اقلیدسی فضا  میں سمتیہ کی لمبائی کی تعریف یوں ہو جائے گی (اقلیدسی فضا پر "اندرونی حاصل ضرب" کی پہلی تعریف استعمال کرتے ہوئے):
میں سمتیہ کی لمبائی کی تعریف یوں ہو جائے گی (اقلیدسی فضا پر "اندرونی حاصل ضرب" کی پہلی تعریف استعمال کرتے ہوئے):

دیکھو کہ یہ اقلیدسی ہندسہ (Euclidean geometry) میں لمبائی کی تعریف ہے۔ غور کرو کہ فضا پر "اندرونی حاصل ضرب" کی تعریف بدلنے سے "لمبائی" کی تعریف بھی مختلف ہو گی۔
فضا میں فاصلہ[ترمیم]
تفصیلی مضمون : فاصلہ (ریاضی)
لکیری فضا میں دو سمتیوں  اور
اور  (فضا میں دو نکتوں) کے درمیان فاصلہ
(فضا میں دو نکتوں) کے درمیان فاصلہ  یوں تعریف کیا جاتا ہے :
یوں تعریف کیا جاتا ہے :

اقلیدسی فضا میں فاصلہ[ترمیم]
اقلیدسی فضا  میں فاصلے کی تعریف یوں ہو سکتی ہے (اقلیدسی فضا پر "اندرونی حاصل ضرب" کی پہلی تعریف استعمال کرتے ہوئے):
میں فاصلے کی تعریف یوں ہو سکتی ہے (اقلیدسی فضا پر "اندرونی حاصل ضرب" کی پہلی تعریف استعمال کرتے ہوئے):

دیکھو کہ یہ اقلیدسی ہندسہ میں دو نکتوں کے درمیان فاصلے کی تعریف ہے۔ غور کرو کہ فضا پر "اندرونی حاصل ضرب" کی تعریف بدلنے سے "فاصلے " کی تعریف بھی مختلف ہو گی۔
اندرونی حاصل ضرب" کی مزید خصوصیات[ترمیم]
"اندرونی حاصل ضرب" کی تعریف سے کچھ مزید خصوصیات اخذ کی جا سکتی ہیں ( ،
،  اور
اور  ، سمتیہ ہیں، جبکہ
، سمتیہ ہیں، جبکہ  ایک سکیلر):
ایک سکیلر):





قائم الزاویہ[ترمیم]
| اصطلاح
|
term
|
| قائم الزاویہ
|
Orthogonal
|
دو سمتیہ  اور
اور  کو قائم الزاویہ کہا جائے گا اگر ان کا "اندرونی حاصل ضرب" صفر ہو، یعنی
کو قائم الزاویہ کہا جائے گا اگر ان کا "اندرونی حاصل ضرب" صفر ہو، یعنی

اگر سمتیہ  کا مجموعہ
کا مجموعہ  میں تمام سمتیوں سے "اندرونی حاصل ضرب" صفر ہو، تو سمتیہ
میں تمام سمتیوں سے "اندرونی حاصل ضرب" صفر ہو، تو سمتیہ  کو مجموعہ
کو مجموعہ  سے قائم الزاویہ کہا جاتا ہے۔
سے قائم الزاویہ کہا جاتا ہے۔
فیثاغورث" مسئلہ اثباتی[ترمیم]
تصویر میں فضا  کی مثال
کی مثال
 |
اگر سمتیہ  اور
اور  قائم الزاویہ ہوں، یعنی
قائم الزاویہ ہوں، یعنی

تو:

قائم امثول[ترمیم]
| اصطلاح
|
term
|
| قائم امثول
|
Orthonormal
|
ایک "اندرونی حاصل ضرب فضا" پر سمتیہ مجموعہ  ، جس میں ہر سمتیہ دوسرے سے قائیم الزاویہ ہو اور ہر سمتیہ کا امثولہ ایک (1) ہو، ایسے سمتیہ مجموعہ کو قائم امثول بولتے ہیں۔ یعنی
، جس میں ہر سمتیہ دوسرے سے قائیم الزاویہ ہو اور ہر سمتیہ کا امثولہ ایک (1) ہو، ایسے سمتیہ مجموعہ کو قائم امثول بولتے ہیں۔ یعنی

اور

جسے یوں بھی لکھا جا سکتا ہے

قائم امثول" بنیاد سمتیہ مجموعہ کے حوالے سے صورت[ترمیم]
کسی"اندرونی حاصل ضرب فضا" پر  اگر ایک "قائم امثول" بنیاد سمتیہ مجموعہ ہو، تو اس فضا کے کسی سمتیہ
اگر ایک "قائم امثول" بنیاد سمتیہ مجموعہ ہو، تو اس فضا کے کسی سمتیہ  کو اس مجموعہ کے حوالے سے یوں لکھا جا سکتا ہے :
کو اس مجموعہ کے حوالے سے یوں لکھا جا سکتا ہے :

یعنی سمتیہ u کی صورت اس بنیاد سمتیہ مجموعہ S کے حوالے سے n اعداد سے ظاہر کی جاتی ہے، جسے (یعنی n اعداد کو) ہم میٹرکس کے بطور یوں لکھ سکتے ہیں :
![{\displaystyle \ u=\left[{\begin{matrix}\langle u,v_{0}\rangle \\\langle u,v_{1}\rangle \\\vdots \\\langle u,v_{n-1}\rangle \end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/241f8bc2b8faf77cb8ea2b66e297964722b748c2)
 فضا میں "قائم الزاویہ بنیاد سمتیہ مجموعہ" کے حوالے سے فضا کے کسی سمتیہ کی صورت نکالنے کا طریقہ ہم دیکھ چکے ہیں۔ اس مسئلہ اثباتی کی خوبی یہ ہے کہ یہ کسی بھی سمتیہ فضا (جہاں "اندرونی حاصل ضرب" تعریف ہوا ہو) کے لیے طریقہ بتاتا ہے۔ یہ بھی خیال رہے کہ اگر بنیاد سمتیہ مجموعہ قائم الزاویہ نہ ہو تو صورت نکالنے کے طریقہ میں یکلخت لکیری مساوات کا حل نکالنے کی دشواری کا سامنا کرنا پڑتا ہے۔
فضا میں "قائم الزاویہ بنیاد سمتیہ مجموعہ" کے حوالے سے فضا کے کسی سمتیہ کی صورت نکالنے کا طریقہ ہم دیکھ چکے ہیں۔ اس مسئلہ اثباتی کی خوبی یہ ہے کہ یہ کسی بھی سمتیہ فضا (جہاں "اندرونی حاصل ضرب" تعریف ہوا ہو) کے لیے طریقہ بتاتا ہے۔ یہ بھی خیال رہے کہ اگر بنیاد سمتیہ مجموعہ قائم الزاویہ نہ ہو تو صورت نکالنے کے طریقہ میں یکلخت لکیری مساوات کا حل نکالنے کی دشواری کا سامنا کرنا پڑتا ہے۔
مسلئہ اثباتی[ترمیم]
کسی"اندرونی حاصل ضرب فضا"، جس کا بُعد n ہو۔ اس فضا پر  ایک "قائم امثول" بنیاد سمتیہ مجموعہ ہو۔ اس فضا کے کسی سمتیہ
ایک "قائم امثول" بنیاد سمتیہ مجموعہ ہو۔ اس فضا کے کسی سمتیہ  اور
اور  کو اس مجموعہ کے حوالے سے یوں لکھا گیا ہو:
کو اس مجموعہ کے حوالے سے یوں لکھا گیا ہو:
![{\displaystyle \mathbf {u} =\left[{\begin{matrix}u_{0}\\u_{1}\\\vdots \\u_{n-1}\end{matrix}}\right]\,,\,\,\mathbf {w} =\left[{\begin{matrix}w_{0}\\w_{1}\\\vdots \\w_{n-1}\end{matrix}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd1d08b6f23bfaebe4f177851ba7d2df69e55c19)
تو سمتیہ کے امثولہ، فاصلہ اور "اندرونی حاصل ضرب" کو یوں دیا جاتا ہے :



اس مسئلہ اثباتی کی خوبی یہ ہے کہ یہ  فضا جیسے خوبصورت نتائج کسی بھی سمتیہ فضا (جہاں "اندرونی حاصل ضرب" تعریف ہوا ہو) کے لیے عام کرتا ہے۔
فضا جیسے خوبصورت نتائج کسی بھی سمتیہ فضا (جہاں "اندرونی حاصل ضرب" تعریف ہوا ہو) کے لیے عام کرتا ہے۔
مسلئہ اثباتی[ترمیم]
کسی"اندرونی حاصل ضرب فضا" پر مجموعہ  میں تمام n غیر صفر سمتیہ "قائم امثول" ہوں (تمام سمتیہ ایک دوسرے کے ساتھ قائم الزاویہ ہوں اور ہر سمتیہ کا امثولہ ایک (1) ہو)، تو
میں تمام n غیر صفر سمتیہ "قائم امثول" ہوں (تمام سمتیہ ایک دوسرے کے ساتھ قائم الزاویہ ہوں اور ہر سمتیہ کا امثولہ ایک (1) ہو)، تو
- یہ سمتیہ مجموعہ لکیری آزاد ہو گا۔
قائم امثول بنیاد سمتیہ مجموعہ (مسلئہ اثباتی)[ترمیم]
لکیری فضا، جس میں "اندرونی حاصل ضرب" تعریف ہوا ہو اور اس کا بُعد محدود ہو۔ ایسی لکیری فضا میں "قائم امثول بنیاد سمتیہ مجموعہ" ہمیشہ موجود ہوتا ہے۔
ایک "بنیاد سمتیہ مجموعہ" سے "قائم امثول بنیاد سمتیہ مجموعہ" گرام شمٹ طریقہ سے نکالا جا سکتا ہے۔ اس طریقہ میں مسقط (نیچے دیکھو) کی مدد سے مجموعہ سے قائم امثول مجموعہ کشید کیا جاتا ہے۔
| اصطلاح
|
term
|
مسقط
تقرب
|
Projection
Approximation
|
- تفصیلی مضمون: مسقط (ریاضی)
مسقط مسئلہ اثباتی[ترمیم]
اگر U کسی "اندرونی حاصل ضرب فضا" V کی لکیری ذیلی فضا ہو، تو V کے کسی بھی سمتیہ v کو صرف ایک منفرد صورت میں یوں لکھا جا سکتا ہے :

جبکہ سمتیہ u "ذیلی فضا" U میں ہو اور سمتیہ b "ذیلی فضا" U کے قائم الزاویہ ہو۔ اب سمتیہ u کو سمتیہ v کا مسقط (projection) کہا جاتا ہے۔

تصویر میں  فضا میں سمتیہ v دکھایا گیا ہے۔ (اس فضا کو جیومیٹری میں معکب XYZ کہا جا سکتا ہے۔ ) اس سمتیہ کا مسقط سمتیہ u ہے، جو فضا
فضا میں سمتیہ v دکھایا گیا ہے۔ (اس فضا کو جیومیٹری میں معکب XYZ کہا جا سکتا ہے۔ ) اس سمتیہ کا مسقط سمتیہ u ہے، جو فضا  (جیومیٹری میں XY پلین) میں ہے۔ غور کرو کہ سمتیہ u اور سمتیہ b ایک دوسرے سے نوے درجہ کے زاویہ (قائم الزاویہ) پر ہیں۔ دراصل سمتیہ b اور پلین XY آپس میں قائم الزاویہ ہیں (یعنی سمتیہ b، پلین XY میں کسی بھی سمتیہ سے نوے درجہ کا زاویہ بناتا ہے)۔ سمتیہ b کو اکثر غلطی سمتیہ کہا جاتا ہے۔
(جیومیٹری میں XY پلین) میں ہے۔ غور کرو کہ سمتیہ u اور سمتیہ b ایک دوسرے سے نوے درجہ کے زاویہ (قائم الزاویہ) پر ہیں۔ دراصل سمتیہ b اور پلین XY آپس میں قائم الزاویہ ہیں (یعنی سمتیہ b، پلین XY میں کسی بھی سمتیہ سے نوے درجہ کا زاویہ بناتا ہے)۔ سمتیہ b کو اکثر غلطی سمتیہ کہا جاتا ہے۔
مسلئہ اثباتی (بہترین تقرب)[ترمیم]
اگر U کسی "اندرونی حاصل ضرب فضا" V کی لکیری ذیلی فضا ہو، تو V کے کسی بھی سمتیہ v کا ذیلی فضا U میں مسقط  ، سمتیہ v کا بہترین تقرب ہے، اس معنی میں کہ
، سمتیہ v کا بہترین تقرب ہے، اس معنی میں کہ

جہاں u ذیلی فضا U کا کوئی بھی دوسرا سمتیہ ہے۔
یعنی مسقط کے غلطی سمتیہ

کا امثولہ سب سے کم ہو گا- یہ ہم پہلے ہی دیکھ چکے ہیں کہ یہ غلطی سمتیہ e قائم الزاویہ ہوتا ہے ذیلی فضا U کے (یعنی U میں تمام سمتیوں کے )۔
"اندرونی حاصل ضرب" کی مدد سے ہم مسقط نکال سکتے ہیں۔
مسلئہ اثباتی[ترمیم]
ایک "اندرونی حاصل ضرب فضا" V کی لکیری ذیلی فضا U ہو۔ اگر فضا U کے لیے  ایک قائم امثول بنیاد سمتیہ مجموعہ ہو، تو فضا V کے کسی بھی سمتیہ z کا مسقط
ایک قائم امثول بنیاد سمتیہ مجموعہ ہو، تو فضا V کے کسی بھی سمتیہ z کا مسقط  ذیلی فضا U میں یوں نکالا جا سکتا ہے :
ذیلی فضا U میں یوں نکالا جا سکتا ہے :

- مثال: فضا
 میں سمتیہ
میں سمتیہ ![{\displaystyle z=\left[{\begin{matrix}2\\2\\2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4946ad86ec55c94a9ab78545188ff5115bc6626)
کا پلین XY میں مسقط نکالتے ہیں۔ پلین XY کے لیے
![{\displaystyle v_{0}=\left[{\begin{matrix}1\\0\\0\end{matrix}}\right]\,,\,\,v_{1}=\left[{\begin{matrix}0\\1\\0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df504cb77d56eeb2aae098f9989cdfc41956f43e) ایک قائم امثول بنیاد سمتیہ مجموعہ ہے۔ اب
ایک قائم امثول بنیاد سمتیہ مجموعہ ہے۔ اب


![{\displaystyle {\hbox{proj}}_{\{XYplane\}}z=2v_{0}+2v_{1}=\left[{\begin{matrix}2\\2\\0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/256953f05425f9e377980ed2969ee52d4a71020d)
مزید دیکھیے[ترمیم]
E=mc2 اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے ریاضی علامات











![{\displaystyle \mathbf {u} =\left[{\begin{matrix}u_{0}\\u_{1}\\\vdots \\u_{n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7979838a30debfcc4f08509bc160e07af4b422)
![{\displaystyle \mathbf {v} =\left[{\begin{matrix}v_{0}\\v_{1}\\\vdots \\v_{n-1}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44ec0b66ead11ed07c9a79ed69e71ff2067d349d)







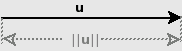

























![{\displaystyle \ u=\left[{\begin{matrix}\langle u,v_{0}\rangle \\\langle u,v_{1}\rangle \\\vdots \\\langle u,v_{n-1}\rangle \end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/241f8bc2b8faf77cb8ea2b66e297964722b748c2)


![{\displaystyle \mathbf {u} =\left[{\begin{matrix}u_{0}\\u_{1}\\\vdots \\u_{n-1}\end{matrix}}\right]\,,\,\,\mathbf {w} =\left[{\begin{matrix}w_{0}\\w_{1}\\\vdots \\w_{n-1}\end{matrix}}\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd1d08b6f23bfaebe4f177851ba7d2df69e55c19)












![{\displaystyle z=\left[{\begin{matrix}2\\2\\2\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4946ad86ec55c94a9ab78545188ff5115bc6626)
![{\displaystyle v_{0}=\left[{\begin{matrix}1\\0\\0\end{matrix}}\right]\,,\,\,v_{1}=\left[{\begin{matrix}0\\1\\0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df504cb77d56eeb2aae098f9989cdfc41956f43e)


![{\displaystyle {\hbox{proj}}_{\{XYplane\}}z=2v_{0}+2v_{1}=\left[{\begin{matrix}2\\2\\0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/256953f05425f9e377980ed2969ee52d4a71020d)