دائرہ

دائرہ

مستوی کے کسی ایک معین (Fixed) نقطہ سے ہم فاصلہ تمام نقاط کے سیٹ کو دائرہ کہتے ہیں۔

معین نقطہ اس دائرے کا مرکز اور اور اس نقطہ سے دائرے کے کسی بھی نقطہ کو ملانے والے قطہ خط کو رداسی قطعہ Radial Segment اور اس کی لمبائی کو رداس Radius کہتے ہیں۔
اس لحاظ سے:

• دائرہ کا مرکز اس کے اندر واقع ہوتا ہے۔
• کسی دائرے کا مرکز یکتا ہوتا ہے۔
• کسی دائرے کے تمام رداس لمبائی میں برابر ہوتے ہیں۔

دائرہ کا محیط

کسی دائرہ کے مرکز سے رداس کے فاصلہ پر موجود تمام نقاط کو ملانے والے خط یعنی دائرے کی لمبائی کو دائرے کا محیط کہتے ہیں۔

دائرہ کا وتر

دائرہ کا وتر اور قطر

ایسا قطعہ خط جس کے دونوں سرے دائرہ کے نقاط ہوں اس دائرے کا وتر کہلاتا ہے۔ جیسا کہ اس شکل میں دائرہ کا مرکز O ہے، قطعہ خط PQ اور LM دائرہ کے وتر ہیں۔

دائرہ کا قطر

دائرے کے مرکز میں سے گزرتا ہوا وتر دائرے کا قطر کہلاتا ہے۔ جیسا کہ اس شکل میں دائرہ کا مرکز O ہے، قطعہ خط PQ اور LM دائرہ کے وتر ہیں جبکہ LM دائرے کا قطر ہے کینوکہ یہ دائرے کے مرکز O سے گزرتا ہے۔

دائرہ کی قوس

دائرے کے محیط کا کوئی بھی ٹکڑا یا حصہ دائرے کی قوس کہلاتا ہے۔ جیسا کہ اس شکل میں PQ کو دائرہ کی قوس کہیں گے۔

نصف دائرہ

کسی دائرے کے مرکزی وتر سے کٹا ہوا نصف محیط پر مشتمل شکل یا حصہ نصف دائرہ کہلاتا ہے۔ جیسا کہ اس شکل میں PQ نصف دائرہ کو ظاہر کرتا ہے۔

قوس صغیرہ

ایسی قوس جو نصف دائرہ سے چھوٹی ہو دائرہ کی قوس صغیرہ کہلاتی ہے۔ جیسا کہ اس شکل میں PQ ایک قوس صغیرہ ہے۔

قوس کبیرہ

ایسی قوس جو نصف دائرہ سے بڑی ہو دائرہ کی قوس کبیرہ کہلاتی ہے۔ جیسا کہ اس شکل میں RS ایک قوس کبیرہ ہے۔

مرکزی زاویہ

کوئی قوس دائرہ کے مرکز پر جو زاویہ بناتی ہے اس کو مرکزی زاویہ کہتے ہیں۔ جیسا کہ اس شکل میں قوس AB دائرے کے مرکز C پر زاویہ ACB بناتی ہے جو قوس AB کا مرکزی زاویہ ہے۔

متماثل دائرے اور قوسیں

وہ دائرے جن کے رداس برابر ہوں متماثل دائرے کہلاتے ہیں۔
ایسی دو قوسیں جو ایک ہی دائرے یا دو متماثل دائروں پر واقع ہوں اور جن کی لمبائیاں برابر ہوں متماثل قوسیں کہلاتی ہیں۔

اس لحاظ سے:

کسی بھی دائرہ یا دو مختلف متماثل دائروں میں دو قوسیں متماثل ہوں گی اگر ان کے مرکزی زاویے متماثل ہوں گے۔

دائرہ کا قطعہ

دائرہ کا قطعہ

دائرہ کا وتر دائروی علاقہ کو دو حصوں میں تقسیم کرتا ہے۔ یہ علاقے دائرہ کے قطعات کہلاتے ہیں۔
وتر اور قوس صغیرہ کا محصور علاقہ قطعہ صغیرہ جبکہ وتر اور قوس کبیرہ کا محصور علاقہ قطعہ کبیرہ کہلاتا ہے۔
سامنے کی شکل میں گہرا سایہ دار علاقہ قطعہ صغیرہ جبکہ باقی علاقہ قطعہ کبیرہ ہے۔
اس لحاظ سے:

• قطعہ صغیرہ نصف دائروی علاقہ سے چھوٹا ہوتا ہے۔
• قطعہ کبیرہ نصف دائروی علاقہ سے بڑا ہوتا ہے۔

دائرہ کا سیکٹر

دائرہ کا سیکٹر

دائرہ کے کوئی سے دو رداسی قطعات اور ان کے متعلقہ قوس سے گِھرا ہوا دائروی علاقہ دائرہ کا سیکٹر کہلاتا ہے۔ سامنے کی شکل میں OPQ اور OPR دائرے کے سیکٹر ہیں۔
اس لحاظ سے:

• کسی دائروی علاقہ کو ایک سے زیادہ سیکٹرز میں تقسیم کیا جا سکتا ہے۔
• کسی مستوی پر ایک خط مستقیم اور ایک دائرے کی موجودگی کی مندرجہ ذیل تین صورتیں ممکن ہیں۔
  • جب خط مستقیم دائرہ کو دو نقاط پر قطع کرے۔
  • جب خط مستقیم دائرہ کو ایک نقطع پر مَس کرے۔
  • جب خط مستقیم دائرہ کو کہیں بھی مَس یا قطع کرے۔

دائرہ کا خط قاطع

ایسا خط مستقیم جو کسی دائرہ کو دو نقاط پر قطع کرے خط قاطع کہلاتا ہے۔

دائرہ کا مماس

ایسا خط مستقیم جو دائرے کے محیط کو صرف اور صرف ایک نقطہ پر مَس کرے اور اس پر موجود کوئی اور نقطہ دائرے کے اندرونہ میں واقع نہ ہو دائرے کا مماس کہلاتا ہے جیسا کے اوپر کی شکل میں دائرہ C₂ میں خط دکھایا گیا ہے۔
دائروں کی شکل میں خط AB دائرہ C₁ کا خط قاطع
دائرہ C₂ کا مماس
اور دائرہ C₃ کا خط قاطع ہے نہ مماس۔
اس لحاظ سے:

• دائرہ کا ہر رداس اس کے محیط کو صرف ایک نقطہ پر قطع کرتا ہے لیکن یہ دائرے کا مماس نہیں ہے۔

مماسہ دائرے

مماسہ دائرے

وہ دائرے جو ایک دوسرے کو صرف اور صرف ایک نقطہ پر مَس کریں مماسہ دائرے کہلاتے ہیں۔
دو دائرے ایک دوسرے کو دو طرح سے مَس کر سکتے ہیں۔

• جب ایک دائرہ دوسرے دائرے کے اندر ہو۔
• جب ایک دائرہ دوسرے دائرے کے باہر ہو۔

مشترک مماس

دائروں کے مشترک نقطہ پر خط مماس ان دائروں کا مشترک مماس کہلاتا ہے۔

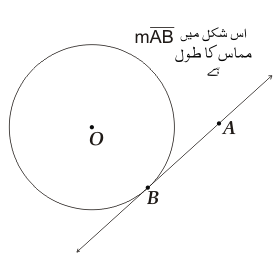
مماس کا طول

کسی بیرونی نقطہ سے دائرہ کے کسی نقطہ پر مماس کھینچا جائے تو ان نقاط کا درمیانی فاصلہ مماس کا طول کہلاتا ہے۔
اس لحاظ سے:

• دو مماسہ دائروں کے مرکز اور نقطہ مماس ایک ہی خط مستقیم پر واقع ہوتے ہیں۔

ہم مرکز دائرے

ایسے دائرے جن کا مرکز ایک ہی نقطہ ہو ہم مرکز دائرے کہلاتے ہیں۔
اوپر کی شکل میں تمام دائروں کا مرکز O ہے پس تمام دائرے ہم مرکز ہیں۔

مثلث کے حوالے سے دائروں کی اقسام

مثلث کے حوالے سے دائروں کی مندرجہ ذیل تین اقسام ہیں۔

مثلث کا محاصرہ دائرہ

ایسا دائرہ جو مثلث کے تینوں راسوں میں سے گزرے مثلث کا محاصرہ دائرہ کہلاتا ہے۔ اس دائرہ کا مرکز اس کا مرکزِ محیط کہلاتا ہے اور اس کا رداس محیط رداس کہلاتا ہے۔ انگریزی میں اسے عام طور پر R سے ظاہر کیا جاتا ہے۔
سامنے دی گئی شکل میں O دائرے کا مرکزِ محیط اور R رداس ہے۔

دائرے کا مرکزِ محیط دی گئی مثلث کے اضلاع کے عمودی ناصفوں کا مشترک نقطہ تقاطع ہوتا ہے۔

اس لحاظ سے:

• مثلث کے تینوں عمودی ناصف مرکزِ محیط پر آپس میں ایک دوسرے کو ایک مشترک نقطہ پر قطع کرتے ہیں۔
  

مثلث ABC کے اضلاع کے عمودی ناصف مشترک نقطہ O پر قطع کرتے ہیں۔

مثلث کا محصور دائرہ

ایسا دائرہ جو مثلث کے تینوں اضلاع کو اندرونی طور پر مَس کرے مثلث کا محصور دائرہ کہلاتا ہے۔ اس کا رداس محصور رداس کہلاتا ہے۔ انگریزی میں اسے عام طور پر r سے جبکہ محصور مرکز کو I سے ظاہر کرتے ہیں۔
سامنے کی شکل میں دیا گیا دائرہ مثلث ABC کا محصور دائرہ، IP محصور رداس اور نقطہ I محصور مرکز ہے۔
اس لحاظ سے:

• محصور دائرہ کا مرکز I مثلث کے تینوں اضلاع سے ہم فاصلہ ہے۔
• مثلث کے تینوں زاویوں کے ناصف مرکز I پر ایک دوسرے کو قطع کرتے ہیں۔

مثلث کا جانبی دائرہ

کسی مثلث کے دو اضلاع کو بڑھایا جائے تو ایسا دائرہ جو مثلث کے ایک ضلع کو بیرونی طور پر اور دوسرے بڑھے ہوئے دونوں اضلاع کو اندرونی طور پر مَس کرے مثلث کا جانبی دائرہ کہلاتا ہے۔ ایسے دائرے کا مرکز جانبی مرکز اور رداس جانبی رداس کہلاتا ہے۔
سامنے دی گئی شکل میں مثلث ABC کے اضلاع AC اور AB کو نقاط 'B اور 'C تک بڑھایا، ایک دائرہ جس کا مرکز I₁ ہے مثلث ABC کے ضلع BC کو باہر سے نقطہ P پر اور 'AC اور 'AB کو نقاط Q اور R پر اندر کی طرف سے مَس کرتا ہے۔
شکل میں دکھایا گیا ہے کہ دائرہ مثلث ABC کا جانبی دائرہ ہے اور mI₁P=r₁ دائرہ کا جانبی رداس ہے
اس لحاظ سے:

• دائرہ کا مرکز I₁ مثلث کے راس A کی مخالف سمت میں ہے۔
• اندرونی زاویہ A اور بیرونی زاویوں 'GBB∠ اور C'CB∠ کے ناصف نقطہ I₁ پر قطع کرتے ہیں جو جانبی دائرے کا جانبی مرکز ہیں۔