توضیحی فنکشن

x کی منفی اقدار کے لیے اَسٔی فنکشن تقریباً مسطح (آہستہ چڑھتی) ہوتی ہے، x کی مثبت اقدار کے لیے تیزی سے چڑھتی ہے اور x=0 کے لیے 1 کے برابر ہوتی ہے۔ اس کی y قدر ہمیشہ نقطہ x پر اس کی مائل کے برابر ہوتی ہے۔

اصطلاح	term
اَسّی تفاعل مائل	exponential function slope

ریاضیات میں اَسّی فنکشن ایک دالہ ہے۔ اس فنکشن کے قدر x پر اطلاق کو $\ \exp(x)$ لکھا جاتا ہے۔ یا بمعادلہ اس کو e^x لکھا جاتا ہے، جہاں e ریاضیاتی دائم ہے جو قدرتی لاگرتھم کی اساس ہے (تقریباً 2.718281828)۔

ایک حقیقی متغیر کی فنکشن کے بطور، y = e^x کا گراف ہمیشہ مثبت ہوتا ہے (x محور سے اوپر) اور بڑھتا ہوا (بائیں سے دائیں دیکھتے ہوئے)۔ یہ x محور کو کبھی نہیں چھوتا، اگرچہ یہ اس کے من مانا قریب آ سکتا ہے۔ (گویا، x محور اس گراف کا افقی asymptote ہے)۔ اس کا اُلٹا دالہ قدرتی لاگرتھم $\ \ln(x)$ ہے، جو مثبت x کے لیے تعریف شدہ ہے۔

سائنس میں "اَسّی تفاعل" ہیئت cb^x کی فنکشن کو بھی کہتے ہیں، جہاں b، جسے اساس کہتے ہیں، کوئی مثبت حقیقی عدد ہو، ضروری نہیں کہ e۔

جامع طور پر، متغیر x حقیقی یا مختلط عدد ہو سکتا ہے۔

بالامنظر اور تشویق

اَسّی فنکشن کو ریاضیاتی دائم e کو طاقت x پر چڑھانے صورت میں لکھا جاتا ہے کیونکہ جب اسی فنکشن کا اطلاق 1 پر کیا جائے تو جواب e ہوتا ہے،

$\,\exp(1)=e$

اور یہ اسٔاتی شناخت

$\,\exp(x+y)=\exp(x)\cdot \exp(y)\$

پر پورا اترتی ہے۔

یہ منفرد متواصل فنکشن ہے جو حقیقی عدد طاقت کے لیے ان دو شناختوں کی تسکین کرتی ہے۔ اس وجہ سے اسے غیرناطق طاقت پر چڑھانے کے عمل کی تعریف میں استعمال کیا جاتا ہے۔

جب z مخلوط عدد ہو تو اَسّی فنکشن $e^{z}$ کی مختلط مستوی میں کہیں بھی وحدانیت نہیں ہوتی۔ اسّی فنکشن کا عائلر کلیہ میں اظہار اسے مختلط اعداد کے ساتھ کام کرنے میں مرکزی اہمیت کا حامل بنا دیتا ہے۔

اَسّی فنکشن کی مختلف توصیف ہیں۔ جو توصیف اس کے ریاضی میں نفوذی استعمال کی وجہ ہے یہ ہے کہ ایسی فنکشن ہے جس کی تبدیلی کی شرح اس کی قدر کے برابر ہوتی ہے اور جو 0 پر 1 ہے۔ جامع طور پر جہاں تبدیلی کی شرح راست متناسب ہو قدر کے (بجائے برابر ہونے کے )، تو ایسی فنکشن کا اَسّی فنکشن کے ذریعہ یوں اظہار کیا جا سکتا ہے :

$f'(x)=kf(x)\ ,$

$f(0)=c\ ,$

دیتا ہے

$f(x)=ce^{kx}\ .$

اگر b = e^k تو اس کی ہیئت یوں cb^x ہوتی ہے۔ اسّائیا کسی جامع اساس b پر، جیسے b^x (کو اَسّی فنکشن اساس b پر بولتے ہیں) کو اَسّی فنکشن اور اس کے اُلٹ، لاگرتھم، کے استعمال سے یوں تعریف کیا جاتا ہے :

$\,\!\,b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\ln b}.\,$

سائنس میں اس کے استعمال سے اَسّائی نُمُو اور اَسّائی تنزل تشریح کیا جاتا ہے۔

صَوّری تعریف

اَسّی تفاعل (نیلا) اور طاقت سلسلہ کی پہلی n+1 اصطلاحات کا حاصل جمع (سرخ)

اَسّی فنکشن e^x کو انواع مساوی طریق سے تعریف کیا جا سکتا ہے، بطور لامتناہی سلسلہ کے۔ خاص طور پر طاقت سلسلہ کے طور پر یوں :

$e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots$

اس تعریف کی ہیئت ٹیلر سلسلہ کی ہے۔

بعض اوقات e^x کو درج ذیل مساوات کے حل y کے بطور تعریف کیا جاتا ہے

$x=\int _{1}^{y}{dt \over t}$

اس کی درج ذیل حد بھی ہے :

$e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}$

مختلط مستوی پر

مختلط مستوی پر اَسّی فنکشن۔ گہرے سے ہلکے رنگوں کی طرف تغیر ظاہر کرتا ہے کہ اَسّی فنکشن کی مطلق قدر بڑھ رہی ہے، دائیں طرف۔ میعادی افقی شریط (پٹی) ظاہر کرتے ہیں کہ اَسّی فنکشن اپنے ادخال کے تخیلی حصہ میں میعادی ہے۔

حقیقی اعداد کے معاملہ کی طرح، مختلط مستوی میں بھی اَسّی فنکشن کو مختلف مساوی طریقہ سے تعریف کیا جا سکے ہے۔ طاقت سلسلہ سے تعریف کی جا سکتی ہے، حقیقی عدد کو مختلط عدد سے بدل کر:

$\,\!\,e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}$

اس کو مد نظر رکھتے ہوئے باآسانی دیکھا جا سکتا ہے کہ کیوں ${d \over dz}e^{z}=e^{z}$ تمام مختلط مستوی پر لاگو ہے۔

ایک اور تعریف جو حقیقی معاملہ کو مختلط پر وسعت دیتا ہے۔ پہلے ہم آرزو وصف بیان کرتے ہیں۔ $e^{x+iy}=e^{x}e^{iy}$۔ اب $e^{x}$ کے لیے ہم حقیقی اَسّی فنکشن ہی استعمال کرتے ہیں۔ پھر ہم تخیلی حصہ کے لیے تعریف کرتے ہیں : $\ e^{iy}=cos(y)+isin(y)$

جب مختلط مستوی پر تعریف کیا جائے تو اَسّی فنکشن اپنی اہم خصوصیات برقرار رکھے ہے : $\,\!\,e^{z+w}=e^{z}e^{w}$

$\,\!\,e^{0}=1$

$\,\!\,e^{z}\neq 0$

$\,\!\,{d \over dz}e^{z}=e^{z}$

تمام (مختلط) z اور w کے لیے۔

یہ فنکشن میعادی ہے، تخیلی میعاد $\,2\pi i$ پر اور یوں لکھا جا سکتا ہے

$\,\!\,e^{a+bi}=e^{a}(\cos b+i\sin b)$

جہاں a اور b حقیقی عدد ہیں۔ یہ کلیہ اَسّی فنکشن کو مثلثیاتی دالہ سے تعلق دیتا ہے۔ اس طرح ہم دیکھتے ہیں کہ تمام ابتدائی دالہ سوائے کثیر رقیم کے، اَسّی فنکشن سے پھوٹتے ہیں ایک یا دوسرے راستے سے۔ قدرتی لاگرتھم کو مختلط مد میں وسعت دینے سے متعدد قدری دالہ $\ \ln(z)$ ملتی ہے۔ اس سے ہم جامع اَسّیاتی تعریف کر سکتے ہیں :

$\,\!\,z^{w}=e^{w\ln z}$

مختلط عدد z اور w کے لیے۔ یہ بھی متعدد قدری فنکشن ہے۔ اوپر دیے اسیاتی قوانین سچ رہتے ہیں اگر متعدد قدری فنکشن کی صحیح تشریح کی جائے۔ چونکہ یہ متعدد قدری فنکشن ہے، حقیقی عدد کے لیے اَسّیائی کا ضرب دینے کا کلیہ کام نہیں کرتا،

$\,\!\,(e^{z})^{w}\neq e^{\left(zw\right)}$

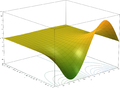
اَسّی فنکشن مختلط مستوی میں کسی لکیر کو مختلط مستوی میں لاگرتھمی گردش میں لے جاتی ہے جس کا مرکز مبدا ہوتا ہے۔

• مختلط مستوی پر اَسّی دالہ کے گراف
• 
  z = Re(e^x+iy)
• 
  z = Im(e^x+iy)
• 
• 

مختلط z کے لیے exp(z) کی شمارندگی

$z=x+iy$ کے لیے یہ سیدھا سادھا کلیہ ہے

$\,e^{x+yi}=e^{x}e^{yi}=e^{x}(\cos(y)+i\sin(y))=e^{x}\cos(y)+ie^{x}\sin(y)$

یہاں مثلثیاتی فنکشن کا استدلال y حقیقی ہے۔

ab کی شمارندگی جب a اور b مختلط ہوں

مختلط اَسّیاتی a^b کو تعریف کرنے کے لیے a کو قطبی متناسق میں بدل کر اور یہ شناخت (eln(a))b = ab استعمال کر کے :

$\,a^{b}=(re^{{\theta }i})^{b}=(e^{\ln(r)+{\theta }i})^{b}=e^{(\ln(r)+{\theta }i)b}$

البتہ جب b صحیح عدد نہ ہو، تو یہ فنکشن متعدد رقمی ہوتی ہے کیونکہ θ منفرد نہیں ہوتا۔

مزید دیکھیے

• Matrix function

E=mc2     اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے     ریاضی علامات