نظریۂ حرکیہ نظامات
| اصطلاح | term |
|---|---|
|
حرکیہ نظام |
dynamic system |
نظریۂ حرکیہ نظامات علاقہ ہے اطلاقی ریاضیات کا جو پچیدہ حرکیہ نظامات کا طرزِ عمل بیان کرتا ہے، عموماً تفرقی مساوات یا فرق مساوات کے استعمال سے۔ جب تفرقی مساوات کی خدمات حاصل کی جائیں، تو نظریہ کو استمری حرکیہ نظامات کہتے ہیں۔ جب فرق مساوات کی خدمات لی جائیں تو نظریہ کو متفرد حرکیہ نظامات کہا جاتا ہے۔ جب وقت متغیر ایسے طاقم پر چلے جو کچھ وقفوں پر متفرد ہو اور دوسرے وقفوں پر استمری یا تعسُفی طاقم ہو جیسے کانٹر طاقم، تو ہم کو ملتا ہے حرکیہ مساوات وقتی میزانوں پر۔ کچھ صورتحالوں کو آمیزش عالجوں جیسے تفرقی-فرق مساوات سے تمثیل کیا جا سکتا ہے۔
یہ نظریہ معاملہ کرتا ہے حرکیہ نظام کے لمبی-مدت کفیتی طرزِعمل سے اور حرکت مساوات کے حل کا مطالعہ کرتا ہے ان نظامات کا جو اولٰی آلاتی نوعیت کے ہوتے ہیں؛ اگرچہ ان میں شامل ہیں دونوں سیارہ کے مدار اور برقیات دوران کا طرز عمل اور جُزوی تفرقی مساوات کے حل جو حیاتیات میں اُٹھتے ہیں۔ حالیہ برسوں میں اس میدان میں بہت سی تحقیق شواشی نظامات پر مرکوز ہوئی ہے۔
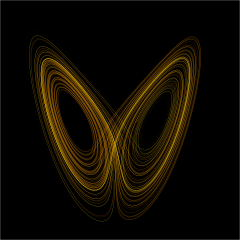
جائزہ[ترمیم]
نظریہ حرکیہ نظام اور نظریہ شواش معاملہ کرتے ہیں حرکیہ نظام کے لمبی-مدّت کیفیتی طرزِعمل سے۔ یہاں مرکوز حرکیہ نظام کو بیان کرنے والی مساوات کے قطعی حل ڈھونڈنا نہیں (جو اکثر غیر اُمیدی ہوتا ہے)، بلکہ اس طرح کے سوالوں کا جواب دینا "کیا نظام لمبے مدّتی کسی ثباتی حالت میں سکونت اختیار کر لے گا اور اگر ہاں، تو ممکنہ ثباتی حالتیں کونسی ہیں؟" یا "کیا نظام کا لمبے-مدّت طرزِ عمل اس کی آغازی حالت پر منحصر ہے؟"
ایک اہم مقصد حرکیہ نظام کے مستقل نقطے بیان کرنا ہے یا نظام کی ثباتی حالتیں؛ یہ متغیروں کی وہ اقدار ہیں جو وقت کے ساتھ تبدیل نہیں ہوں گی۔ ان میں سے کچھ مستقل نقطے کششی ہیں، مطلب کہ اگر نظام کسی قریبی حالت میں آغاز کرتا ہے، تو اس مستقل نقطہ کی طرف مرتکز ہو گا۔
اسی طرح ہم میعادی نقطوں میں دلچسپی رکھتے ہیں، نظام کی وہ حالتیں جو اپنے آپ کو کئی وقت-قدموں کے بعد دہراتی ہیں۔ میعادی نقاط کششی بھی ہو سکتے ہیں۔ سارکوسکی قضیہ یک بُعد متفرد حرکیہ نظام کے میعادی نقاط کی تعداد بارے دلچسپ بیان ہے۔
سادہ لالکیری حرکیہ نظام بھی اکثر قریباً تصادفی، بالکل ناقابلِ پیشنگوئی طرزِ عمل کا مظاہرہ کرتے ہیں جسے شواش کہا گیا ہے۔ حرکیہ نظام کی وہ شاخ جو شواش کی شفاف تعریف اور تفتیش سے معاملہ کرتی ہے، نظریہ شواش کہلاتی ہے۔
| اصطلاح | term |
|---|---|
|
نسبت |
relation |
تاریخ[ترمیم]
نظریۂ حرکیہ نظامات کی ابتدائیییاں نیوٹن میکانیات میں ہیں۔ وہاں، جیسا کہ دوسری قدرتی علوم اور ہندسیہ میں، حرکیہ نظام کے ارتقا کا قاعدہ مضمر طور پر ایک نسبت سے دیا جاتا ہے جو نظام کی حالت قلیل وقت مستقبل میں کے لیے بتاتا ہے۔
تیز رفتار شمارندی آلات کی آمد سے پہلے، حرکیہ نظام کے حل کے لیے ثقیف ریاضیاتی تکانیک کی ضرورت پڑتی تھی اور حرکی نظامات کی قلیل جماعت کے لیے ہی یہ سر انجام دینا ممکن تھا۔
تصورات[ترمیم]
حرکیہ نظامات[ترمیم]
حرکیہ نظام کا تصور ریاضیاتی رسمیات ہے کسی مستقل قاعدہ کے لیے جو کسی نقطہ کے اپنی محاصری فضاء میں مقام کی وقت تابعیت بیان کرتا ہے۔ مثالوں میں شامل ہے ریاضیاتی تماثیل جو جُھلاتے ہوئے نواس گھڑی کو بیان کرتے ہیں، نلی میں بہتے پانی کے بہاؤ کو اور بہاریہ جھیل میں مچھلیوں کی تعداد کو۔
حرکیہ نظام کی ایک حالت ہوتی ہے جو حقیقی اعداد کے مجموعہ سے جبر ہوتی ہے یا جامع طور پر مناسب حالت فضاء میں نقاط کے طاقم سے۔ نظام کی حالت میں چھوٹی تبدیلیاں ارتباط کرتی ہیں اعداد میں چھوٹی تبدیلیوں سے۔ یہ اعداد ہندسہ فضاء، ایک مشاعب، کے متناسق بھی ہوتے ہیں۔ حرکیہ نظام کا ارتقا قاعدہ ایک مستقل قاعدہ ہوتا ہے جو بتاتا ہے کہ موجودہ حالت سے کونسی مستقبل کی حالتیں آئیں گی۔ یہ قاعدہ جبری ہوتا ہے: کسی دیے وقت وقفہ کے لیے موجودہ حالت سے صرف ایک مستقبل حالت رونما ہو گی۔
لالکیری نظام[ترمیم]
ریاضیات میں لالکیری نظام ایسے نظام کو کہتے ہیں جو لکیری نہ ہو، یعنی یہ نظام اصولِ تَطَبُّق کی تسکین نہ کرتا ہو۔ آسان الفاظ میں، لالکیری نظام ایسا ہوتا ہے جس کے متغیر(وں) جن کا حل مقصود ہو کو انفرادی اجزاء کے لکیری حاصل جمع کے طور پر نہیں لکھا جا سکتا۔ ہمجنس نظام، جو لکیری ہو سوائے کہ آزاد متغیر کی فنکشن کی موجودگی کے، کڑی تعریف کے تحت لالکیری ہے، مگر ایسے نظاموں کو لکیری کے ساتھ مطالعہ کیا جاتا ہے، کیونکہ ان کو لکیری نظام میں استحالہ کیا جا سکتا ہے اگر آزاد متغیر کی فنکشن کے ارتباط والا متخصص حل معلوم ہو۔
نسبتی میدان[ترمیم]
نظریۂ شواش[ترمیم]
نظریہ شواش ایسے حرکیہ نظامات – نظامات جن کی حالت وقت کے ساتھ ارتقا پزیر ہو – کا بیاں کرتا ہے جو ایسی حرکیہ مظہر کرتے ہیں جو آغازی حالات پر بالا حساس ہوں (عرف عام میں اسے تتلی اثر کہا جاوے ہے)۔ اس حساسی کی بنا پر، جو آغازی حالت میں قلق کی اَسّی نمّو کے طور آشکار ہوتے ہیں، شواشی نظامات کا طرز عمل تصادفی معلوم ہوتا ہے۔ یہ ان نظامات کے جبری ہونے کے باوجود مظہر ہوتا ہے۔ جبری سے مرآد ہے کہ ان کی حرکیات ان کی آغازی حالت سے مکمل طور پر تعریف ہو جاتی ہیں اور کوئی تصادفی عنصر شامل نہیں ہوتے۔ اس طرزِعمل کو جبری شواش یا صرف شواش بولتے ہیں۔
پیچیدہ نظامات[ترمیم]
پیچیدہ نظامات سائنسی میدان ہے، جو ایسے نظامات کے مشترکہ خاصوں کا مطالعہ کرتا ہے جنہیں فطرت، معاشرہ اور سائنس میں پچیدہ سمجھا جاتا ہے۔ اسے نظریہ پیچیدہ نظامات، پیچیدگی سائنس بھی کہا جاتا ہے۔ ان کے مطالعہ میں کلیدی مسائل ان کے رسمی تمثیل اور تشبیہ میں مشکلات ہیں۔ اس نکتہ نظر سے، مختلف تحقیقی سیاق و سباق میں پیچیدہ نظامات اپنے مختلف خاصوں کے اساس پر تعریف کیے جاتے ہیں۔
پیچیدہ نظامات کا مطالعہ سائنس کے بہت سے علاقوں میں نئی حیوی لا رہا ہے جہاں مثالی تخفیفی حربے کم پڑ گئے تھے۔ پیچیدہ نظامات اس لیے بطور ایک وسیع تر اصطلاح استعمال ہوتی ہے جو متنوع شعبہ جات میں تحقیقی انداز کو گھیرتی ہے، جس میں شامل ہیں عصبیات، معاشرتی سائنسیں، علمِ موسمیات، کیمیا، طبیعیات، شمارندی سائنس، نفسیات، مصنوعی زندگی، ارتقائی شمارندی، اقتصادیات، زلزلہ پیشن گوئی، سالماتی حیاتیات اور خود زندہ خلیات کی فطرت کی پُرسِش۔
نظریۂ تظبیط[ترمیم]
نظریہ تظبیط ایک بین الشعبہ شاخ ہے ہندسہ اور ریاضیات کی، جو حرکیہ نظامات کے طرزِ عمل پر اثر انداز (ان کو تظبیط کرنے) ہونے سے متعلق ہے۔
نظریۂ ارغودگی[ترمیم]
نظریہ ارغودگی شاخ ہے ریاضیات کی جو غیر متبدل ناپ والے حرکیہ نظامات اور متعلقہ مسائل کا مطالع کرتی ہے۔ اس کی ابتدائی ترقی احصائی طبیعیات سے تحریک پائی تھی۔
